Sample Targeted Activities (3-6)
Algebraic Reasoning
Algebraic reasoning is about noticing patterns and being able to describe these patterns using mathematical language. It is a way of thinking relationally.
An example of algebraic reasoning suggests that a student who is thinking relationally is able to recognize the equivalence of 3(x+4) and 3x+12 by focusing on the structures without the need for solving the problem step by step.
The ability to learn to find and extend numerical patterns to develop relational thinking is dependent on how students are taught and should be a significant component of a student’s learning of mathematics. It is important for students to understand the equal sign means “balance” or “same as”.
Resources
PDF Instructions and Activities
Expression Matching Overview Video
Expression Matching Demonstration Video
Activity 1
Determine what goes in the blank. Try to think relationally.
27 + 8 = __ + 29
16 + __ = 7 + 14
3 + 4 + 3 + 4 = 2 x __
5 (2 + 7) = __ x 5
Activity 2
Match the following numerical expressions with their visual models. (More than one might match)

Fraction Concepts
When building whole number proficiency, the focus is on the units of one. To build fraction proficiency, students must focus on partitioning (or splitting) a unit of one into smaller equal units (e.g., units of halves, fifths, thirds). For example, the very idea that as the denominator of a fraction increases the relative size of the fraction decreases is not a natural understanding for young learners. It takes expressions with models and language to build this understanding.
Resources
PDF Instructions and Activities
Building Fractions with Dice Overview Video
Building Fractions with Dice Demonstration Video
Activity 2
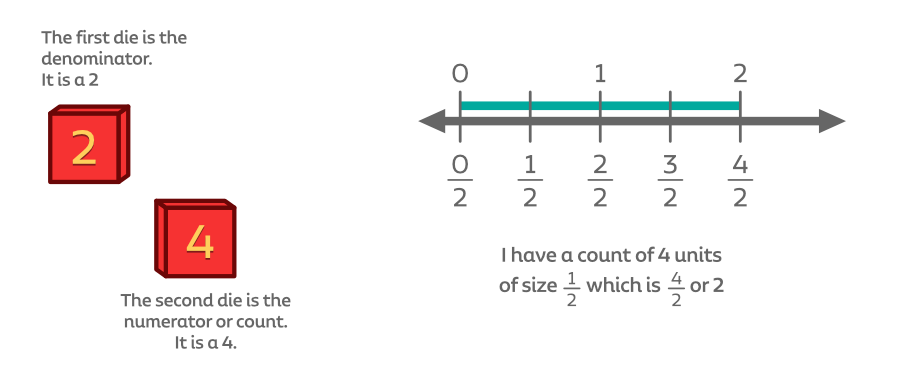
Roll two dice, one at a time.
- The first die is the denominator unit size. Draw a number line from 0 to 1 and partition the number line correctly
- The second die is the numerator. Extend the number line if needed and bold or shade the number line to represent the count
- State how much you have using this sentence structure: "I have a count of ___ units of size which is ___ or ___."
Now try rolling the dice yourself. Create a number line model and use the sentence frame to describe your fraction.
Geometric Measurement
Spatial reasoning is the strongest predictor of future mathematical success. It includes three elements: spatial visualization, spatial orientation, and spatial relations. The first element – spatial visualization – includes the ability to visually or mentally manipulate, rotate, twist, or invert pictorially presented stimuli. The second element is spatial orientation, which involves the ability to remain unconfused when the object’s orientation changes. And the third element – spatial relations – refers to the ability to recognize spatial patterns, understand spatial hierarchies, and imagining maps from verbal descriptions.
Geometry comes from “geo” (the world) and “metry” (to measure). So, geometry is the ability to measure our world in different dimensions (e.g., two- and three-dimensions).
Resources
PDF Instructions and Activities
Floor Tiles Area Activity Overview Video
Floor Tiles Area Activity Demonstration Video
Activity 1
Here is a picture of a pattern of a floor design. Each main tile is 4 inches by 12 inches. Answer the following questions.
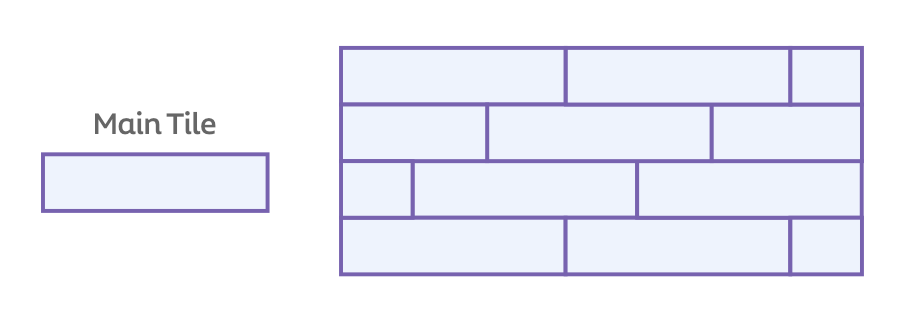
- What patterns do you notice?
- What is the area of this shape in square units?
- What are the dimensions of each of the shapes in the design?
Multiplication & Division Fluency
One key factor contributing to student success in later mathematics is the automation of students’ multiplication facts. There are two critical components to becoming fluent and retaining facts: visualization and flexibility. It is important for students to be able to iterate (copy) and partition (split evenly).
Some students naturally “see” these acts and appear to have memorized their facts when many actually use different strategies very quickly. Students who do not must repeatedly experience those strategies physically and visually to improve their flexibility and ability to retain their multiplication facts.
Resources
PDF Instructions and Activities
Benchmark Using 5's Activity Overview Video
Benchmark Using 5's Activity Demonstration Video
Activity 1
One key factor contributing to student success in later mathematics is the automaticity of students’ multiplication facts. There are two critical components to becoming fluent and retaining facts: visualization and flexibility. It is important for students to be able to iterate (copy) and partition (split evenly). Some students naturally “see” these acts and appear to have memorized their facts when many actually use different strategies very quickly. Students who do not must repeatedly experience those strategies physically and visually to improve their flexibility and ability to retain their multiplication facts.
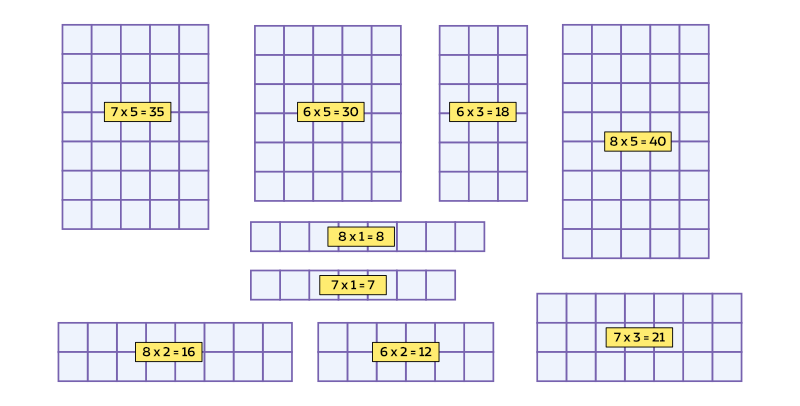
Match the area models with the correct multiplication expressions. There may be more than one way. And you can rotate the area models to fit as necessary.
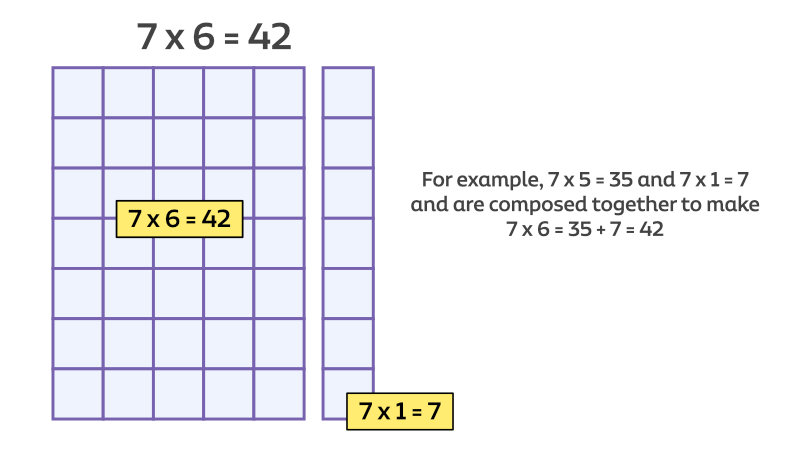
Activity 2
Match the area models with the correct multiplication expressions. There may be more than one way. And you can rotate the area models to fit as necessary.
Place Value & Decimal Concepts
Place value has historically been taught exclusively on the location of digits and their corresponding values. This is not necessarily incorrect, but does limit student learning by ignoring the foundational structure of the Base-10 numeration system. Our place value system is really, and should be taught with, a focus of iterating (copying) a unit 10 times and partitioning (splitting evenly) a unit 10 times. Understanding place value influences the understanding of other mathematical concepts such as number sense, rational numbers, and proportional reasoning.
Decimals are an extension of our place value system when we iterate and partition units less than 1. These numbers should be described in ways that align directly with what students already know about whole numbers. However, the concept of naming decimals by the smallest unit (e.g. .4 is said as “four tenths” but .40 is named “forty hundredths”) is quite unusual for students who have spent most of their early years in school examining whole numbers.
Students must be able to make sense of decimal notation and create visual models to match our notation. As an example, we ask students to recognize and model that 1.3 can be composed of 1 unit of 1 and 3 units of 0.1 and 13 units of 0.1, which also leads to our understanding our standard decimal algorithms for +, –, x, and ÷.
Resources
PDF Instructions and Activities
10 Rule Activity Overview Video
10 Rule Activity Demonstration Video
Activity 1
In this game, you will pick a number card and an increase/decrease card.
You will then state the new number increasing or decreasing its value by a power of 10.
Try these:

Activity 2
Answer the following questions regarding the number 285.7
- What digit is in the hundreds place?
- How much is the digit 8 worth in this number? (Note: the answer is not 8!)
- How many complete tens are in the number?
- What place value is the digit 7 in?
- How many complete tenths are in the number? (Note: the answer is not 7)
Ratio & Proportion Concepts
Proportional reasoning is critical in our everyday life. For instance, if you have a pie recipe that call for 4 Granny Smith apples and 6 Honeycrisp apples, but you want to make 4 pies, then you would need to have 4 times as many Granny Smith apples (16) and 4 times as many Honeycrisp (24). Proportional reasoning means to increase or decrease the entire amount of each element the same multiplicatively.
A bar model is a great visual to keep track of the relationships. For example, if a basketball team has 12 players each on a team. If there were 5 teams, then there would be 60 players total.
Proportional reasoning also applies to shape. For the shape to be in proportion, you have to increase or decrease each of its dimensions by the same amount. So, if a rectangle is 2 x 4 then other rectangles that are in the same proportion could be 4 x 8 (two times larger) or 1 x 2 (1/2 the size).
Resources
PDF Instructions and Activities
Concentration Game Overview Video
Concentration Game Demonstration Video
Activity 1
Determine the quantity of each ingredient required to make a juice recipe for various amounts of people.
Recipe (2 Servings)
- 1 cup orange juice
- 4 mangos
- 6 cups ice
- 1/2 cup sugar
What if we want to make 1 serving? How many of each ingredient?
What if we want to make 5 servings? How many of each ingredient?
Activity 2
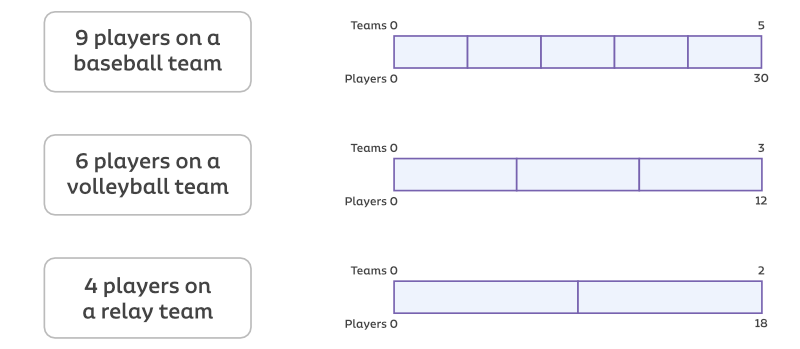
Match each model with the situation by correct ratio of players to teams.
Here is an example with an ice hockey team.
There are 6 players on a hockey team (5 skaters and 1 goaltender)
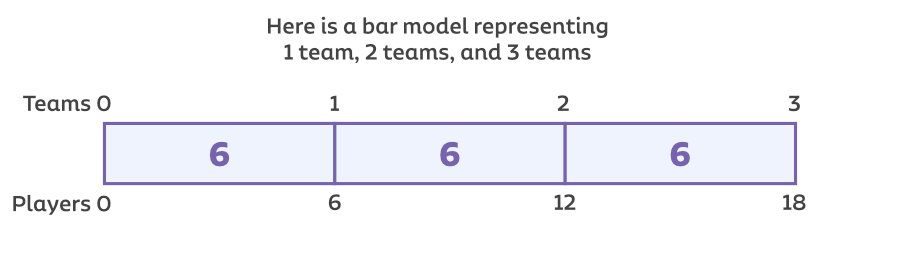
Now try this
Match each model with the situation by the correct ratio of players to teams.