Sample Targeted Activities (K-2)
Interpreting Context
Interpreting contextual problems means to be able to read (or hear) a story or word problem, model it, and then determine an appropriate way to solve it. The more story problems your child solves the better problem-solving skills they acquire.
Contextualized problem-solving requires the ability to understand the underlying problem types (four of them) and related procedures for that class of problems, strong metacognitive skills, and the ability to distinguish relevant information (related to mathematical structure) from irrelevant details. This ability allows a child to see math in everyday situations (e.g., There are 3 birds in the tree. Two are yellow and one is blue. Or there are 6 chairs around the table.)
Resources
PDF Instructions and Activities
Tower Comparison Overview Video
Activity 1
Materials Needed
Blocks or Cubes
Directions
You need two people for this activity.
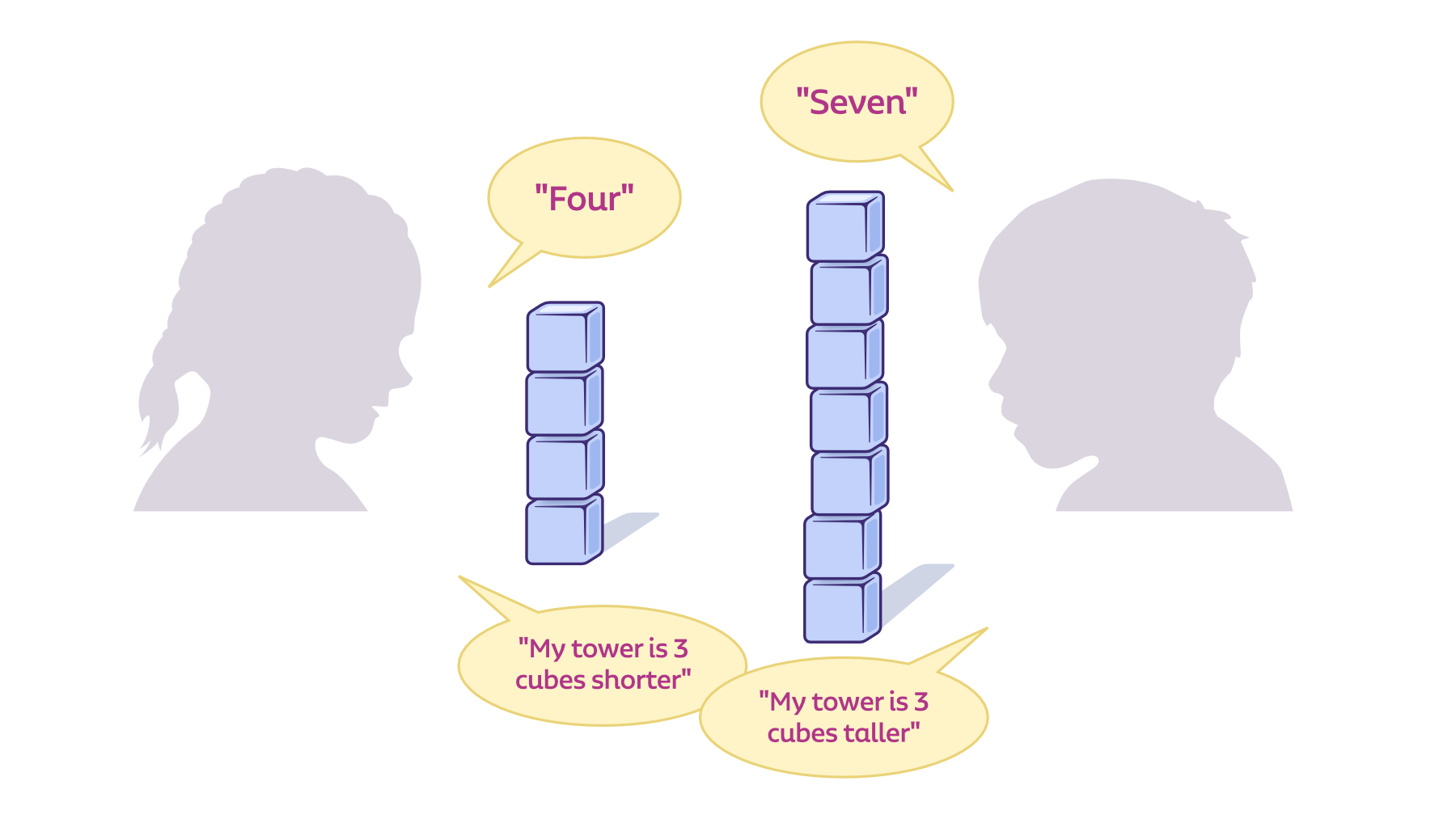
Each person needs to build a tower less than 10 high.
Then you will ask the following questions:
- How tall is your tower?
- How tall is my tower?
- How much taller is the tallest tower than the shorter tower?
Example
Activity 2
Materials Needed
Beach Mat (See PDF)
Directions
Look at this beach scene and use math to describe what you see.
What patterns do you notice?
How many more coconuts in the tree than on the ground?
If you see six rays on the sun, how many might there be if you could see the complete sun?
Measurement
Measurement is one of the most important topics within mathematics and is a very strong predictor of later success. When we measure, we need to understand what unit we will be using to measure an attribute within different areas such as length, area, time, temperature, volume, etc. We then use structural components to examine these relationships.
Unit iteration is the act of repeating a unit to measure an object’s attributes. Partitioning is the act of breaking an object into equal-sized measuring units. Comparative measurement is the process of using a known measurement from one part of an object to find an unknown measurement.
Measurement tasks also support stronger proportional reasoning, which in turn supports understanding of geometry, numeracy and data analysis.
Resources
PDF Instructions and Activities
Quick Draw Demonstration Video
Activity 1
Draw the following shape on a piece of paper or whiteboard
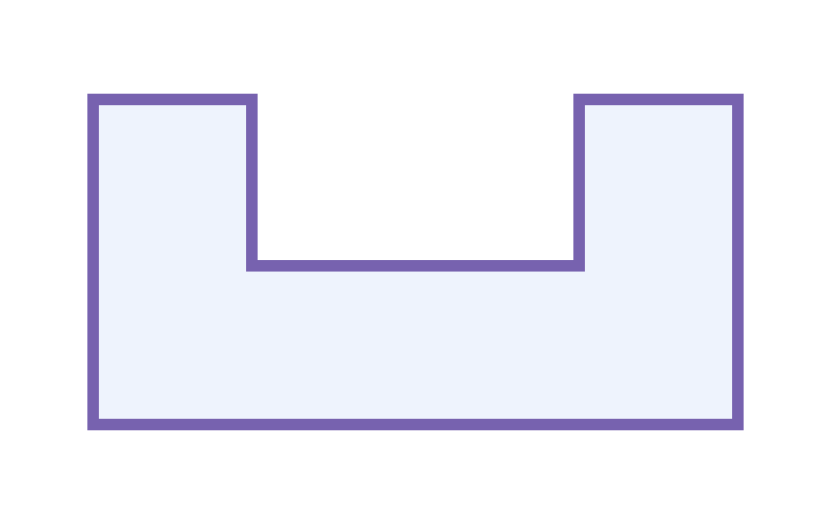
What patterns do you notice?
Find all the sides that are the same.
If the shortest side is 1, then what is the measure of each side of the figure?
If the shorter side is 2, then what is the measure of each side of the figure?
Activity 2
Draw the following shape on a piece of paper or whiteboard

What patterns do you notice?
Find all the sides that are the same.
If the shortest side is 1, then what is the measure of each side of the figure?
If the shortest side is 5, then what is the measure of each side of the figure?
Number Facts
Basic math operations include the ability to add, subtract, multiply and divide single digit and then multi-digit numbers. Fluency with math operations is critical for math achievement throughout a child’s school career and life. If a child learns to retrieve facts in flexible ways, they become more efficient and better problem solvers. One way to impact your child’s thinking is to build spatial-visual representations of the facts and operations in their early years.
Resources
PDF Instructions and Activities
Dice - Addition & Subtraction Demonstration
Activity 1
Materials Needed
Two or three dice. Included in our Math Pack
Directions
Choose 2 or 3 dice to roll.
Add the amounts and state the total.
Example
Roll 3 Dice

3 + 5 = 8
8 + 4 = 12
If your child is younger, they will count each pip (or dot) one by one.
If older, ask your child to state out loud how they flexibly came up with the total.
For instance, "I know 3 plus 5 is 8. Then, I add 8 and 2 to get 10 and then 2 more to get 12".
Activity 2
Materials Needed
4 dice. Included in our Math Pack
Directions
Roll 3 of the dice and add the total.
Roll the 4th die and subtract this amount from the total of the 3 dice.
Example
The first 3 rolls are 5, 17 and 10.

5 + 17 = 22
22 + 10 = 32
The fourth roll is a 4.
32 - 4 = 28
Number Sequencing
Number sense is an important area of mathematical learning in early childhood and includes
- Subitizing, which is to quickly recognize small quantities without counting each item in a set
- Knowing the final count word tells how many are in the set
- Discriminating between small and large quantities
- Comparing numerical magnitudes to determine how much greater or smaller an amount is
- Transforming sets of five or less by adding or taking away items
A key component of number sense is counting or sequencing, which is being able to count forward and backwards. Sequencing is considered a prerequisite for basic operations and seeing and examining patterns or – in upper grades – functions. Success in counting and having number sense in early childhood has been found by researchers to be predictive of later math achievement.
Resources
PDF Instructions and Activities
Tower Building with Dice Video
Activity 1
Materials Needed
One die (per person) and blocks (or cubes or something you can stack)
All available in our Math Pack
Directions
Roll the die.
Grab the number of blocks from the pile that matches the number on the die.
Count how many blocks tall your tower is.
Roll the die again and this time add that number of blocks to your tower and count how tall the tower is now.
Continue this for a few rounds or until the tower collapses.
Relational Thinking
Relational thinking focuses on recognizing patterns across the equal sign and using equivalent transformations to a situation or equation instead of only relying on operations.
For example, a child might be confronted with following problem: 3 + 12 = __ + 4. To use relational thinking to solve for the missing number, a child might say the following. I know that 4 is 1 greater than 3. So, the missing number must be 1 less than 12. The answer is 11.
Researchers have stressed the importance of recognizing and analyzing patterns of equivalence with visual patterns and models, open number sentences, and true/false situations in the early years to bring order and facilitate generalizations in math.
Resources
PDF Instructions and Activities
Dice and Tiles Demonstration Video
Activity 1
Materials Needed
Square tiles or chips. Two or three dice. Included in our Math Pack
Directions
Roll 2 dice.
Use the square tiles to create a row as long as the number on the die.
Creaate another row as long as the number on the other die.
Which row is longer or shorter than the other one? Or are they the same?
How can you make the rows the same?
Example
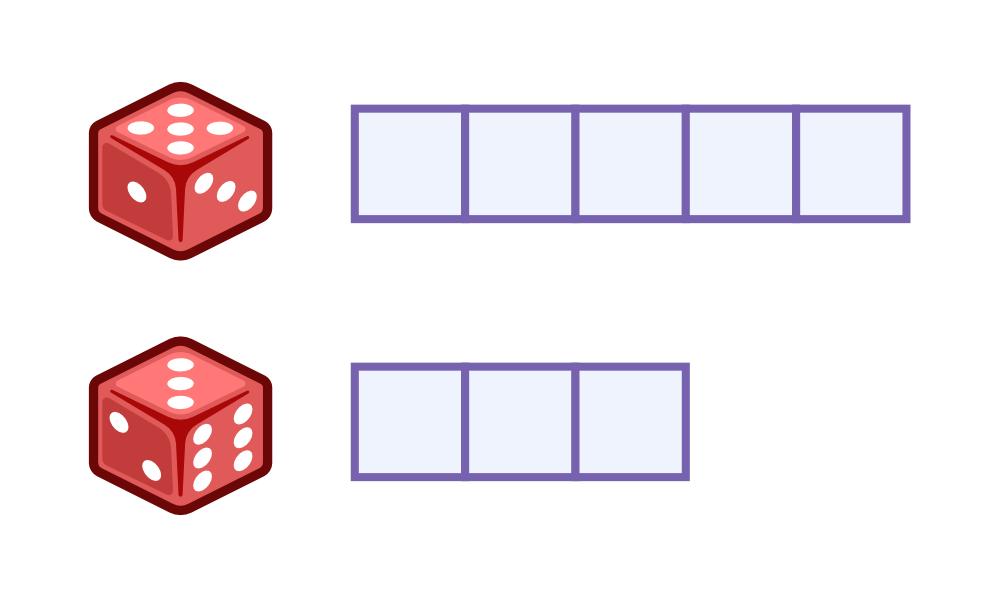
The 5 is longer than the 3.
The 3 is shorter than the 5.
I could add 2 more square tiles to the 3 to make them both 5.
I could take 2 square tiles away from the 5 to make them both 3.
I could take 1 square tile from the row of 5 and give it to the row of 3. Then they would both be 4 tiles long.
Activity 2
Materials Needed
Four dice. Included in our Math Pack
Directions
You are playing against someone else. Each of you will roll 2 dice.
Look for patterns to determine who has the most or least and how to make the same amount.
Example
I rolled an 11 and a 5.
You rolled a 12 and a 3.

I have more because 11 is 1 less than 12, but 5 is 2 more than 3.
If I take two away from the 5, I will have 3.
Then I would give one to the 11 to get 12 and get rid of the other 1.
Then we would both have 12 and 3 or 15 total.
Spatial Reasoning
Spatial reasoning in the early grades is strongly correlated with later achievement in math. Students who perform better on spatial tasks also perform better on tests of mathematical ability.
Spatial reasoning involves:
- spatial visualization, or the ability to mentally manipulate, rotate, twist or invert pictures or objects
- spatial orientation, or the ability to recognize an object even when the object’s orientation changes
- spatial relations, or the ability to recognize spatial patterns, to understand spatial hierarchies, and to imagine maps from verbal descriptions
A child’s ability to visually represent the different topics (e.g., number, geometry, measurement, patterns or functions, and data) increases their ability to remember and solve different types of problems.
Resources
PDF Instructions and Activities
Compose the Square Overview Video
Compose the Square Demonstration Video
Activity 1
Compose the Square
Use these shapes to compose (or put together) a square.
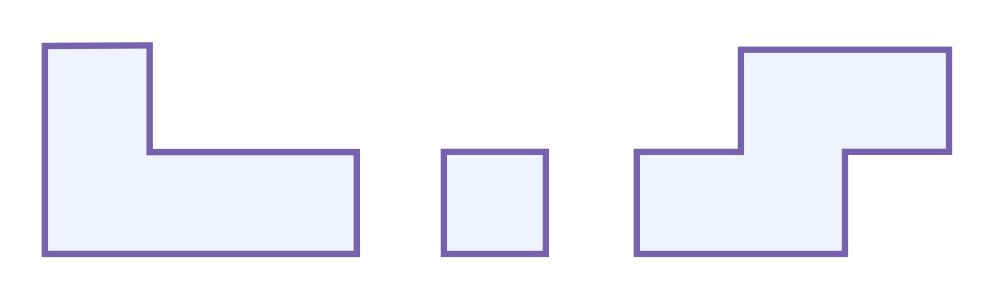
Activity 2
Compose the Square
Use these shapes to compose (or put together) the square.
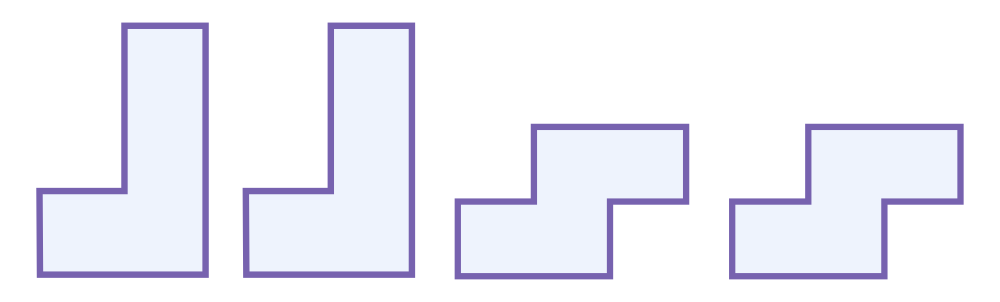
Answers